Automatic group

In mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.

More precisely, let G be a group and A be a finite set of generators. Then an automatic structure of G with respect to A is a set of finite-state automata:

• the word-acceptor, which accepts for every element of G at least one word in A representing it
• multipliers, one for each 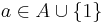, which accept a pair (w₁, w₂), for words w_i accepted by the word-acceptor, precisely when 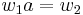in G.

The property of being automatic does not depend on the set of generators.

The concept of automatic groups generalizes naturally to automatic semigroups.

Contents 1 Properties 2 Examples of automatic groups 3 Examples of non-automatic groups 4 Biautomatic groups 5 Automatic structures 6 References

Properties

• Automatic groups have word problem solvable in quadratic time. A given word can actually be put into canonical form in quadratic time.

Examples of automatic groups

• Finite groups, to see this take the regular language to be the set of all words in the finite group.
• Negatively curved groups
• Euclidean groups
• All finitely generated Coxeter groups ^[1]
• Braid groups
• Geometrically finite groups

Examples of non-automatic groups

• Baumslag-Solitar groups
• Non-Euclidean nilpotent groups

Biautomatic groups

A group is biautomatic if it has two multiplier automata, for left and right multiplication by elements of the generating set respectively. A biautomatic group is clearly automatic.^[2]

Examples include:

• A hyperbolic group.^[3]
• An Artin group of finite type.^[3]

Automatic structures

The idea of describing algebraic structures with finite-automata can be generalized from groups to other structures.^[4]

References

1. ^ Brink and Howlett (1993), "A finiteness property and an automatic structure for Coxeter groups", Mathematische Annalen (Springer Berlin / Heidelberg), ISSN 0025-5831. 
2. ^ Birget, Jean-Camille (2000), Algorithmic problems in groups and semigroups, Trends in mathematics, Birkhäuser, p. 82, ISBN 0817641300 
3. ^ ^{a b} Charney, Ruth (1992), "Artin groups of finite type are biautomatic", Mathematische Annalen 292: 671–683, doi:10.1007/BF01444642 
4. ^ Some Thoughts On Automatic Structures, Bakhadyr Khoussainov, Sasha Rubin, 2002

• Epstein, David B. A.; Cannon, James W.; Holt, Derek F.; Levy, Silvio V. F.; Paterson, Michael S.; Thurston, William P. (1992), Word Processing in Groups, Boston, MA: Jones and Bartlett Publishers, ISBN 0-86720-244-0 .
• Chiswell, Ian (2008), A Course in Formal Languages, Automata and Groups, Springer, ISBN 978-1-84800-939-4 .